Die Metrik Halstead Complexity dient der Messung der Komplexität eines Softwareprogramms, ohne dass das Programm selbst ausgeführt werden muss.
Es handelt sich hierbei um eine statische Testmethode, bei der messbare Softwareeigenschaften identifiziert und bewertet werden. Der Quellcode wird analysiert und in eine Reihe von Token untergliedert. Die Token werden dann in Operatoren oder Operanden unterteilt und gezählt.
Die Metrik Halstead Complexity ist von keiner spezifischen Programmiersprache abhängig und kann auf Quellcode nach IEC-61131-3 angewendet werden.
Die Operatoren und Operanden werden folgendermaßen unterteilt und gezählt:
|
Parameter |
Beschreibung |
|---|---|
|
n1 |
Anzahl eindeutiger Operatoren |
|
n2 |
Anzahl eindeutiger Operanden |
|
N1 |
Gesamtanzahl Operatoren |
|
N2 |
Gesamtanzahl Operanden |
Einige Metrikwerte können für verschiedene Komplexitätsaspekte berechnet werden:
oHalstead Difficulty (D)
oHalstead Length (N)
oHalstead CalculatedLength (Nx)
oHalstead Volume (V)
oHalstead Effort (E)
oHalstead Vocabulary (n)
Halstead -Komplexität für in strukturiertem Text (ST) implementierte POUs
Die Halstead-Komplexität wurde ursprünglich für Textsprachen entwickelt (wie C, C++, Pascal usw.) und kann auf in strukturiertem Text (ST) implementierte POUs angewendet werden.
HINWEIS: Standardmäßig wird Halstead Difficulty angezeigt.
Halstead-Komplexität für in Funktionsbausteindiagramm (FBD) implementierte POUs
Das Funktionsbausteindiagramm (FBD) gehört zur Gruppe der grafischen Implementierungssprachen und ist nicht textbasiert. Eine POU setzt sich aus mehreren FBD-Netzwerken zusammen. Die Halstead-Komplexitätsmetrik muss somit angepasst werden, damit sie auf Grafiksprachen angewendet werden kann. Das Basiskonzept ist dasselbe. Operanden und Operatoren sowie deren Häufigkeit (pro FBD-Netzwerk) werden wie für den Benutzer dargestellt berücksichtigt (siehe das Beispiel für Funktionsbausteindiagramm (FBD)).
Die pro FBD-Netzwerk berechneten Halstead-Ergebnisse werden aggregiert und auf POU-Ebene angehängt (Programm, Funktionsbaustein, Funktion, Methode oder Eigenschaft).
HINWEIS: Die berechneten Halstead-Werte (pro FBD-Netzwerk) sind FBD Network Halstead Difficulty und FBD Network Halstead Length.
Die folgenden Aggregationstypen werden pro FBD-Netzwerk auf die Halstead-Metrikwerte (Halstead Difficulty und Halstead Length) angewendet:
oMittelwert
oMinimum
oMaximum
oSumme
oKonsistenz
HINWEIS: Die relevantesten aggregierten Werte sind FBD Halstead Difficulty Network Max, FBD Halstead Difficulty Network Consistency, FBD Halstead Length Network Max und FBD Halstead Length Network Consistency. Alle anderen Kombinationen (Minimum, Summe und Mittelwert) werden ebenfalls berechnet und dem Modell angehängt, jedoch standardmäßig nicht angezeigt.
|
Wert |
Formel |
|---|---|
|
Halstead Difficulty (D) |
D = (n1 / 2) * (N2 / n2) |
|
Halstead Length (N) |
N = N1 + N2 |
|
Halstead CalculatedLength (Nx) |
Nx = n1 * log2(n1) + n2 * log2(n2) |
|
Halstead Volume (V) |
V = N * log2(n) |
|
Halstead Effort (E) |
E = V * D |
|
Halstead Vocabulary (n) |
n = n1 + n2 |
HINWEIS: Ein Ausdruck in einer Anweisung IF <expression> THEN darf keine Klammern enthalten. Diese werden in Quellcode nach IEC-61131-3 als stets verfügbar betrachtet.
Metrikergebnisse wie FBD Network Halstead Difficulty und FBD Network Halstead Length werden für alle FBD-Netzwerke einer POU aggregiert.
values entsprechen der Liste der Werte derselben Metrik (z. B. FBD Network Halstead Length) aller FBD-Netzwerke einer POU).
Der Konsistenzwert ist das Ergebnis des Gini-Koeffizienten. Der Gini-Koeffizient ist ein statistisches Maß zur Darstellung von Ungleichverteilungen bei regelmäßig verteilten Werten. Der Gini-Koeffizient 0 drückt perfekte Gleichverteilung aus, d. h. alle Werte sind identisch. Der Gini-Koeffizient 1 drückt maximale Ungleichverteilung aus.
Beispiel für strukturierten Text (ST)
Halstead-Berechnungsbeispiel für IEC-61131-3-Code (nur der Implementierungsteil wird für die Berechnung berücksichtigt):
IF (xInit = FALSE) THEN
PerformInitialization();
xInit := TRUE;
ELSE
FOR i := 1 TO 5 DO
iAxisId := i + 7;
sAxisName := Standard.CONCAT('MyAxis ', INT_TO_STRING(iAxisId));
// Do some math calculations for each axis here
udiResult := CalculateStuff(sName := sAxisName, iID := iAxisId);
END_FOR
END_IF
Liste der Operatoren und deren Häufigkeit:
Operator Frequency
======== =========
(operators)
If 1
Then 1
LeftParenthesis 6
RightParenthesis 6
Equal 1
Semicolon 5
Assign 7
Else 1
For 1
EndFor 1
Do 1
Plus 1
Period 1
INT_TO_STRING 1
Colon 2
EndIf 1
(n1) 16 (N1) 37
Liste der Operanden und deren Häufigkeit:
Operand Frequency
======= =========
(variables/methods/functions)
xInit 2
PerformInitialization 1
i 2
iAxisId 3
sAxisName 2
Standard 1
CONCAT 1
udiResult 1
CalculateStuff 1
sName 1
iID 1
(constants)
FALSE 1
TRUE 1
INT#1 1
INT#5 1
INT#7 1
'MyAxis ' 1
(n2) 17 (N2) 22
Ergebnis für Halstead Difficulty
Halstead Difficulty (D = (16/2) * (22/17) = 10.3529411764706
Beispiel für Funktionsbausteindiagramm (FBD)
Halstead-Berechnungsbeispiel für in FBD implementierten IEC-61131-3-Code (nur der Implementierungsteil wird für die Berechnung berücksichtigt):
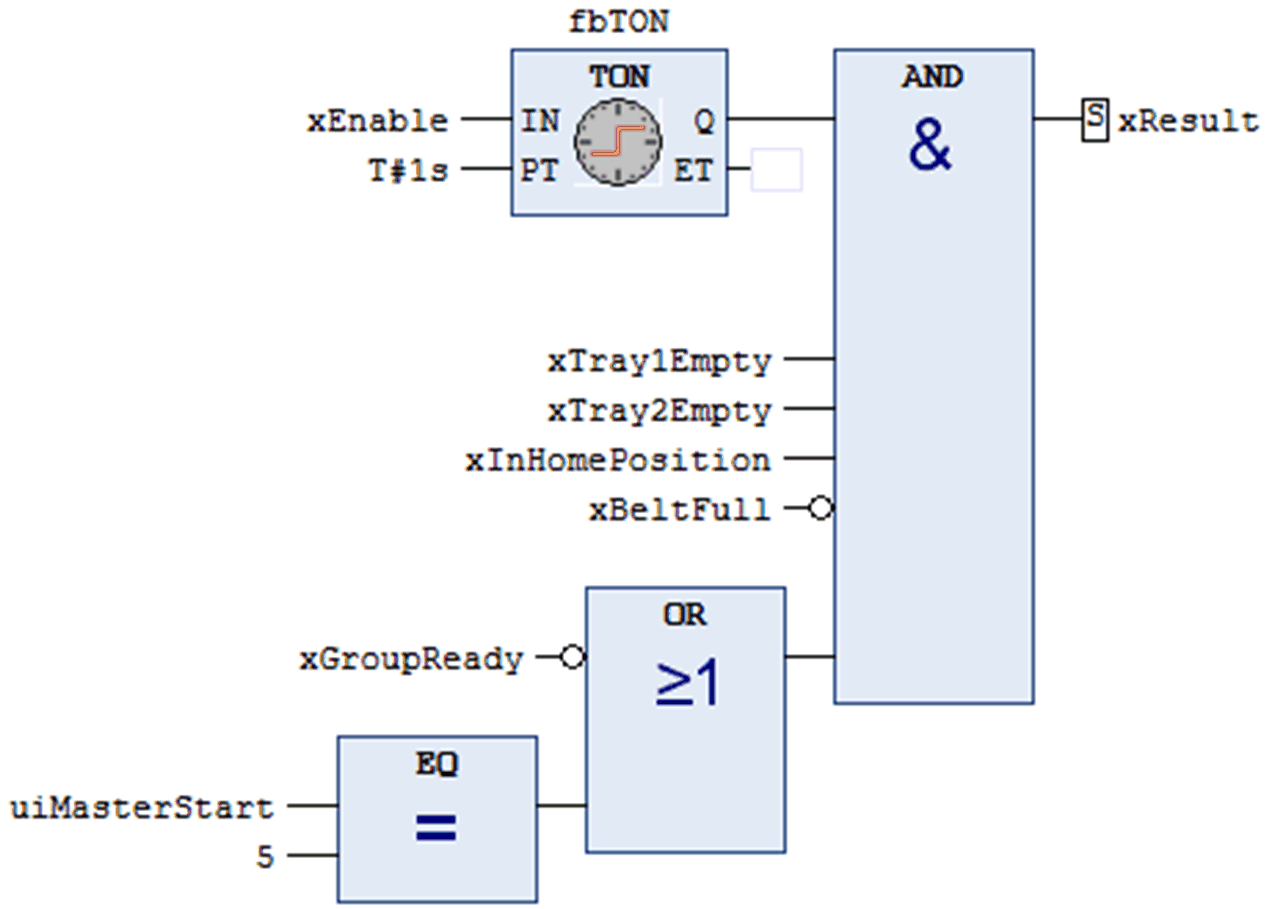
Liste der Operatoren und deren Häufigkeit:
Operator Frequency
======== =========
(operators)
Assign 4
Set2 1
And 1
Negation2 2
Or 1
Eq 1
(n1) 6 (N1) 10
Liste der Operanden und deren Häufigkeit:
Operand Frequency
======= =========
(variables/methods/functions/constants)
xResult 1
TON 1
fbTON 1
xEnable 1
T#1s 1
IN 1
PT 1
Q 1
ET 1
xTray1Empty 1
xTray2Empty 1
xInHomePosition 1
xBeltFull 1
xGroupReady 1
uiMasterStart 1
5 1
(n2) 16 (N2) 16
Ergebnis für FBD Network Halstead Difficulty
FBD Network Halstead Difficulty (D) = (6/2) * (16/16) = 3
FBD Network Halstead Length
FBD Network Halstead Length (D) = 10 + 16 = 26