Orientierungsinterpolation bei CP-Bewegungen
Bei CP-Bewegungen wie MC_MoveLinearAbsolute, MC_MoveLinearRelative, MC_MoveCircularAbsolute oder MC_MoveCircularRelative kann über die Zielposition der Bewegung eine beliebige Zielorientierung des Werkzeugs angegeben werden. Dies hat zur Folge, dass die Orientierung des Werkzeugs während der Bahnbewegung in die Zielorientierung überführt wird, wobei die Werkzeugspitze auf der Bahn verfährt. Es spielt übrigens für die Orientierungsinterpolation keine Rolle, in welchem Koordinatensystem die Zielorientierung angegeben wurde, also beispielsweise in Achskoordinaten (ACS) oder Maschinenkoordinaten (MCS).
Die nachfolgende Abbildung zeigt eine lineare Interpolation mit gleichzeitiger Orientierungsinterpolation. Die roten Pfeile zeigen die Richtung des Werkzeugs am Start- und Endpunkt. Die gestrichelten roten Pfeile zeigen, wie das Werkzeug an einigen Stellen während der Interpolation steht.
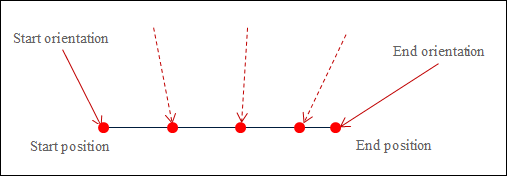
Die oben erwähnten Fuktionsbausteine für Bahnbewegungen besitzen den Eingang OrientationMode. Dieser Eingang definiert, auf welche Art die Startorientierung in die Zielorientierung überführt wird.
Die Großkreisinterpolation (SMC_Orientation_Mode.GreatCircle).
Diese Einstellung ist standardmäßig eingestellt. Dabei wird die Startorientierung auf kürzestem Weg in die Zielorientierung überführt. Der kürzeste Weg bedeutet hier: das Werkzeug wird so in die Zielorientierung gedreht, dass der zurückgelegte Winkel der Drehung minimal ist.
Achsorientierungsinterpolation (SMC_Orientation_Mode.Axis).
Beispiel 1: Großkreisinterpolation
Wir betrachten ein Portal mit einer C-Achse, mit Wertebereich von -360° bis 360°. Die Startorientierung ist bei C=179°, die Zielorientierung bei C=-175°. Die Großkreisinterpolation bewegt die C-Achse der ZYZ-Eulerwinkel (A,B,C) proportional zum zurückgelegten Weg auf der Bahn von 179° in positiver Richtung über 180° bis 185°, was -175° entspricht. Dabei legt sie also einen Gesamtwinkel von 6° zurück.
Beispiel 2: Achsorientierungsinterpolation
Wir betrachten wieder das Portal mit einer C-Achse, dieses Mal mit Wertebereich von -180° bis 180°. Die Startorientierung ist bei C=179°, die Zielorientierung bei C=-175°. Die Achsinterpolation bewegt die C-Achse des Portals proportional zum zurückgelegten Weg auf der Bahn von 179° in negativer Richtung über 0° bis -175°, legt also einen Gesamtwinkel von 354° zurück. (Hätte man in diesem Beispiel die Großkreisinterpolation verwendet, dann wäre es zum Fehler gekommen, da der Arbeitsraum der C-Achse überschritten worden wäre.)
Die beiden Arten der Interpolation unterscheiden sich in einigen wichtigen Eigenschaften
Bei Großkreisinterpolation ist es vorhersagbar, wie sich die Orientierung des Werkzeugs ändert. Bei der Achsinterpolation dagegen ist die Orientierungsänderung nur schwer vorherzusagen, da sich die Orientierungsachsen je nach Stellung unterschiedlich auf die Orientierung auswirken können. Diese Eigenschaft teilt die Achsorientierungsinterpolation mit PTP-Bewegungen. (Das heißt allerdings nicht, dass die Bahn im Raum bei Achsorientierungsinterpolation schwer vorhersagbar wäre: die Bahn ist bei beiden Arten der Orientierungsinterpolation gleich, der TCP verfährt immer exakt die vorgegebene Kontur.)
Mit der Großkreisinterpolation kann man nicht durch Singularitäten der Werkzeugkinematik fahren. Dies geht mit der Achsinterpolation ohne Probleme.
Bei der Großkreisinterpolation kann es zu Verletzungen der Achsgrenzen der Orientierungsachsen kommen, wie im zweiten Beispiel 2 erwähnt. Es ist also erforderlich, bei der Kommandierung sicherzustellen, dass keine Achsgrenzen verletzt werden, wenn die Zielorientierung mit kürzester Drehung angefahren wird.
Mit der Achsinterpolation ist es möglich, um mehr als 360° zu drehen. Wenn eine Orientierungsachse einen Arbeitsraum von mehr als 360° hat, kann man auf diese Art beispielsweise statt zu Position 180° auf 540° fahren. Dies entspricht derselben Orientierung des Werkzeugs. Mit Großkreisinterpolation ist dies nicht möglich, die kürzeste Drehung zur Zielorientierung entspricht ja immer einem Gesamtwinkel von höchstens 180°.
Die Achsinterpolation wird nicht von jeder Kinematik unterstützt. Die Dokumentation der Kinematiken enthält dazu weitere Informationen.
Die Achsinterpolation wird nicht für Tracking-Bewegungen (dynamisches PCS) unterstützt.
Siehe auch
Singularitäten bei Achsorientierungsinterpolation
Mit der Achsorientierungsinterpolation kann eine Bahnbewegung durch die Singularitäten der Werkzeugkinematik erfolgen, was die Programmierung deutlich einfacher machen kann. Dafür ändern sich aber die Singularitäten der Positionierkinematik
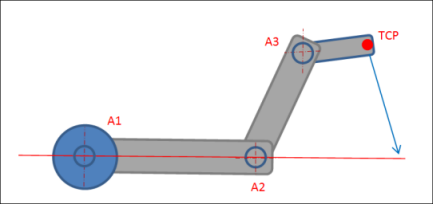
Bei der Großkreisinterpolation hat der Scara3_Z eine Singularität, wenn der Flansch-Punkt (A3) auf der durch den ersten Armteil definierten Geraden liegt, also wenn der zweite Gelenkwinkel 0° beträgt.
Bei der Achsorientierungsinterpolation ändern sich die Singularitäten der Positionierkinematik so, dass der TCP die Rolle einnimmt, die sonst der Flanschpunkt (A3) hat. Sie tritt jetzt auf, wenn der TCP (nicht der Flansch-Punkt) auf der durch den ersten Armteil definierten Geraden liegt. Bei der Kommandierung einer Bewegung mit Achsorientierungsinterpolation wird geprüft, ob zwischen der Start- und der Zielposition der Bewegung diese geänderte Singularität liegt. Falls ja, wird die Bewegung nicht akzeptiert und ein Fehler wird zurückgegeben.
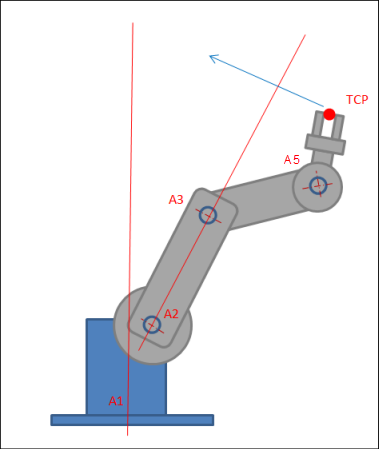
Beim 6-Achs-Knickarmroboter ist die Situation vergleichbar mit dem Scara3_Z, es sind jedoch zwei Singularitäten möglich: Die erste tritt auf, wenn der TCP auf der Geraden durch A2 und A3 liegt, die zweite wenn der TCP auf der Geraden durch A1 liegt. Auch hier wird bei Kommandierung geprüft, dass keine Singularität durchfahren wird.
Info
Es kann vorkommen, dass sich die Konfiguration des Scara3 (oder des 6-Achs-Knickarmroboters) während einer Fahrt mit Achsorientierungsinterpolation ändert. Am Ende der Bewegung wird aber immer dieselbe Konfiguration angenommen, die der Roboter am Startpunkt der Bewegung hatte.