Métrique : Halstead Complexity
La métrique Halstead Complexity est utilisée pour mesurer la complexité d'un programme logiciel sans l'exécuter.
Cette méthode de test statique permet d'identifier et d'évaluer des propriétés mesurables du logiciel. Le code source est analysé et scindé en une suite de jetons, lesquels sont ensuite classés et comptabilisés en tant qu'opérateurs ou opérandes.
La métrique Halstead Complexity ne dépend d'aucune langage de programmation et peut être appliquée au code source IEC-61131-3.
Les opérateurs et les opérandes sont classés et comptabilisés comme suit :
|
Paramètre |
Description |
|---|---|
|
n1 |
Nombre d'opérateurs distincts |
|
n2 |
Nombre d'opérandes distinctes |
|
N1 |
Nombre total d'opérateurs |
|
N2 |
Nombre total d'opérandes |
Plusieurs valeurs de métrique peuvent être calculées pour représenter différents aspects de complexité :
oHalstead Difficulty (D)
oHalstead Length (N)
oHalstead CalculatedLength (Nx)
oHalstead Volume (V)
oHalstead Effort (E)
oHalstead Vocabulary (n)
Métrique Halstead Complexity des POU en langage ST (littéral structuré)
À l'origine, la métrique Halstead Complexity a été développée pour les langages textuels (C, C++, Pascal…). Elle s'applique aux POU en langage ST.
NOTE : La métrique Halstead Difficulty est affichée par défaut.
Métrique Halstead Complexity des POU en langage FBD (diagramme à blocs fonction)
Le langage FBD est un langage d'implémentation graphique ; il n'est pas basé sur du texte. Un POU se compose de plusieurs réseaux FBD. La métrique Halstead Complexity doit être adaptée pour pouvoir s'appliquer aux langages graphiques. Le concept de base est le même. On considère que les opérandes et les opérateurs, ainsi que leur fréquence (par réseau FBD), sont présentés à l'utilisateur (voir la section Exemple en langage FBD).
Les valeurs Halstead Complexity calculées pour chaque réseau FBD sont agrégées pour tous ces réseaux et associées au niveau du POU (programme, bloc fonction, fonction, méthode ou propriété).
NOTE : Les valeurs Halstead calculées (pour chaque réseau FBD) sont FBD Network Halstead Difficulty et FBD Network Halstead Length.
Les types d'agrégation suivants sont appliqués aux métriques Halstead (Halstead Difficulty et Halstead Length) de chaque réseau FBD :
oMoyenne
oMinimum
oMaximum
oSomme
oCohérence
NOTE : Les valeurs agrégées les plus pertinentes sont FBD Halstead Difficulty Network Max, FBD Halstead Difficulty Network Consistency, FBD Halstead Length Network Max et FBD Halstead Length Network Consistency. Les autres combinaisons (minimum, somme et moyenne) sont calculées et associées au modèle, mais ne s'affichent pas par défaut.
|
Valeur |
Formule |
|---|---|
|
Halstead Difficulty (D) |
D = (n1 / 2) * (N2 / n2) |
|
Halstead Length (N) |
N = N1 + N2 |
|
Halstead CalculatedLength (Nx) |
Nx = n1 * log2(n1) + n2 * log2(n2) |
|
Halstead Volume (V) |
V = N * log2(n) |
|
Halstead Effort (E) |
E = V * D |
|
Halstead Vocabulary (n) |
n = n1 + n2 |
NOTE : Une expression contenue dans une instruction IF <expression> THEN ne doit pas avoir de parenthèses. Ces expressions sont considérées comme toujours disponibles dans le code source IEC-61131-3 .
Agrégation des valeurs de la métrique
Les résultats de la métrique, comme FBD Network Halstead Difficulty et FBD Network Halstead Length, sont agrégés pour tous les réseaux FBD d'un POU.
Le paramètre values représente la liste des valeurs d'une métrique (par exemple, FBD Network Halstead Length) pour tous les réseaux d'un POU.
La valeur de cohérence est le résultat du coefficient Gini. Ce coefficient est une mesure de la dispersion statistique, qui sert à mesurer l'inégalité entre les valeurs d'une distribution fréquente. Un coefficient Gini de 0 exprime une égalité parfaite (les valeurs sont toutes identiques). Un coefficient Gini de 1 exprime une inégalité maximale entre les valeurs.
Exemple en langage ST
Exemple de calcul de métrique Halstead pour du code IEC-61131-3 (seule la partie implémentation est prise en compte pour le calcul) :
IF (xInit = FALSE) THEN
PerformInitialization();
xInit := TRUE;
ELSE
FOR i := 1 TO 5 DO
iAxisId := i + 7;
sAxisName := Standard.CONCAT('MyAxis ', INT_TO_STRING(iAxisId));
// Do some math calculations for each axis here
udiResult := CalculateStuff(sName := sAxisName, iID := iAxisId);
END_FOR
END_IF
Liste des opérateurs et de leurs fréquences :
Operator Frequency
======== =========
(operators)
If 1
Then 1
LeftParenthesis 6
RightParenthesis 6
Equal 1
Semicolon 5
Assign 7
Else 1
For 1
EndFor 1
Do 1
Plus 1
Period 1
INT_TO_STRING 1
Colon 2
EndIf 1
(n1) 16 (N1) 37
Liste des opérandes et de leurs fréquences :
Operand Frequency
======= =========
(variables/methods/functions)
xInit 2
PerformInitialization 1
i 2
iAxisId 3
sAxisName 2
Standard 1
CONCAT 1
udiResult 1
CalculateStuff 1
sName 1
iID 1
(constants)
FALSE 1
TRUE 1
INT#1 1
INT#5 1
INT#7 1
'MyAxis ' 1
(n2) 17 (N2) 22
Résultat de la métrique de difficulté Halstead
Halstead Difficulty (D = (16/2) * (22/17) = 10.3529411764706
Exemple en langage FBD
Exemple de calcul de la métrique Halstead pour du code IEC-61131-3 en FBD (seule la partie implémentation est prise en compte pour le calcul) :
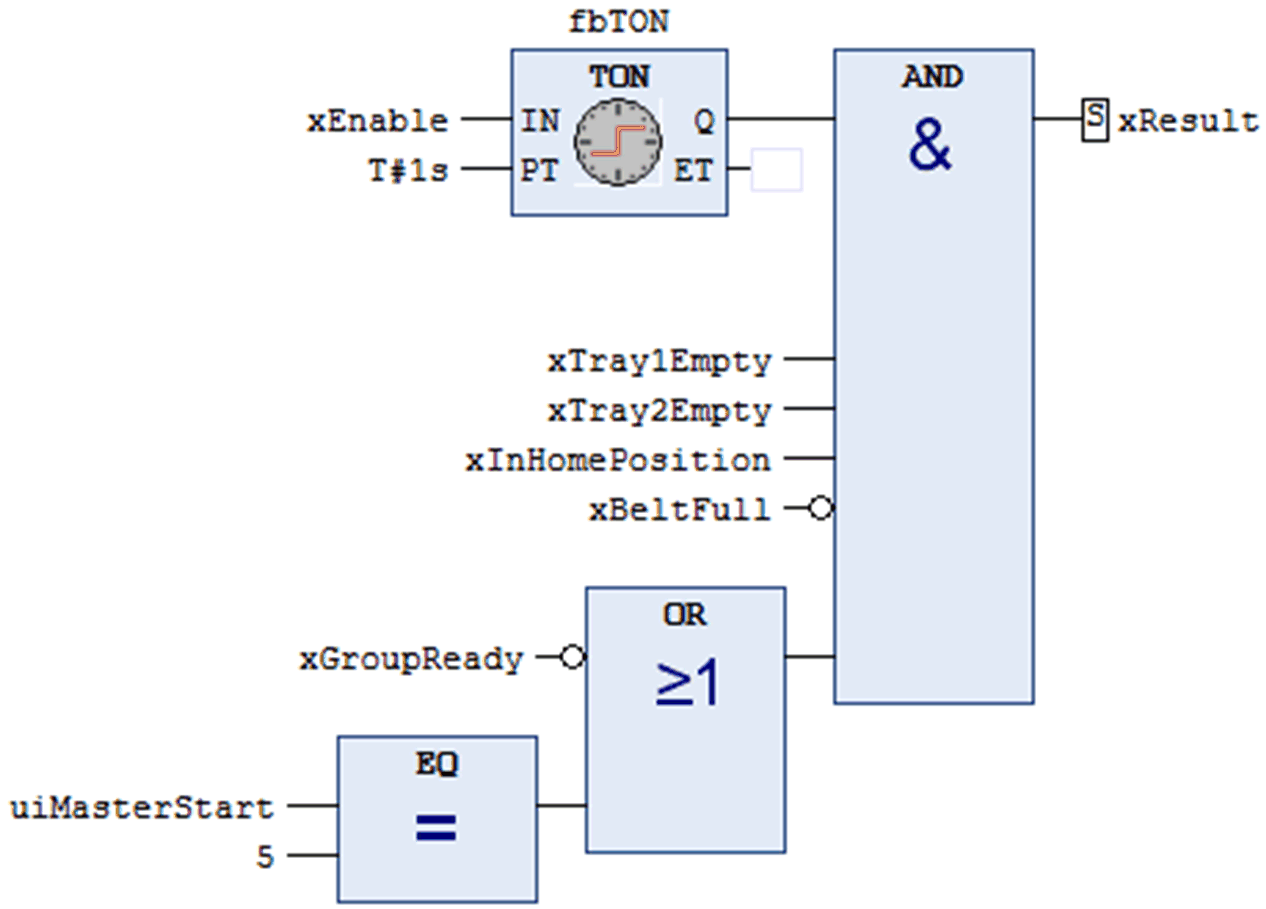
Liste des opérateurs et de leurs fréquences :
Operator Frequency
======== =========
(operators)
Assign 4
Set2 1
And 1
Negation2 2
Or 1
Eq 1
(n1) 6 (N1) 10
Liste des opérandes et de leurs fréquences :
Operand Frequency
======= =========
(variables/methods/functions/constants)
xResult 1
TON 1
fbTON 1
xEnable 1
T#1s 1
IN 1
PT 1
Q 1
ET 1
xTray1Empty 1
xTray2Empty 1
xInHomePosition 1
xBeltFull 1
xGroupReady 1
uiMasterStart 1
5 1
(n2) 16 (N2) 16
Résultat de la métrique FBD Network Halstead Difficulty
FBD Network Halstead Difficulty (D) = (6/2) * (16/16) = 3
Métrique FBD Network Halstead Length
FBD Network Halstead Length (D) = 10 + 16 = 26